
Zadanie Skracalne liczby pierwsze (skr)
Pomóż nam usprawnić bazę zadań!
Skracalne liczby pierwsze
Limit pamięci: 32 MB
Przypomnijmy, że liczba pierwsza to taka dodatnia liczba całkowita, która ma dokładnie dwa różne
dzielniki: jedynkę i samą siebie.
Mówimy, że liczba  jest prefiksem liczby
jest prefiksem liczby  , jeśli liczba
, jeśli liczba  powstaje przez usunięcie pewnej liczby
cyfr z końca liczby
powstaje przez usunięcie pewnej liczby
cyfr z końca liczby  .
Na przykład, liczba
.
Na przykład, liczba  jest prefiksem liczby
jest prefiksem liczby  .
Skracalna liczba pierwsza to taka liczba, której wszystkie prefiksy niezerowej długości są liczbami pierwszymi.
Przykładowo, liczba
.
Skracalna liczba pierwsza to taka liczba, której wszystkie prefiksy niezerowej długości są liczbami pierwszymi.
Przykładowo, liczba 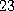 jest skracalną liczbą pierwszą, gdyż jej niepuste prefiksy
jest skracalną liczbą pierwszą, gdyż jej niepuste prefiksy  i
i  są liczbami pierwszymi.
są liczbami pierwszymi.
Twoim zadaniem jest napisanie programu, który dla zadanych dwóch liczb całkowitych dodatnich  ,
,  (
(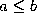 )
wyznaczy, ile jest liczb całkowitych, które są skracalnymi liczbami pierwszymi i należą do domkniętego przedziału
)
wyznaczy, ile jest liczb całkowitych, które są skracalnymi liczbami pierwszymi i należą do domkniętego przedziału  .
.
Wejście
W jedynym wierszu standardowego wejścia znajdują się dwie liczby całkowite  ,
,  (
( ).
).
Możesz założyć, że testach wartych 50% punktów zachodzi dodatkowo warunek  .
.
Wyjście
W jedynym wierszu standardowego wyjścia powinna znaleźć się jedna liczba całkowita będąca liczbą
skracalnych liczb pierwszych nie mniejszych od  i nie większych od
i nie większych od  .
.
Przykład
Dla danych wejściowych:
20 24
poprawną odpowiedzią jest:
1
Wyjaśnienie do przykładu:
W przedziale  jest tylko jedna skracalna liczba pierwsza i jest nią
jest tylko jedna skracalna liczba pierwsza i jest nią  .
.
Autor zadania: Mirosław Michalski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English